Project IMPART — Integrated Modeling and Prediction of Atmospheric Reentry Trajectories

IMPART was my final project for Orbital Mechanics (AE 5626) at The Ohio State University (Fall 2024). The goal was to build a modular, multi-phase framework to model orbital decay, estimate reentry behavior, and set up an eventual impact-dispersion workflow.

1) TL;DR

• Built a three-phase reentry framework in MATLAB + Simulink: orbital decay, reentry dynamics, and footprint concept.
• Compared analytical atmosphere modeling against NRLMSISE-00 (atmosnrlmsise00) across altitude ranges and time-of-day conditions.
• Orbit-decay propagation produced consistent behavior and expected sensitivity trends across mass and initial-altitude cases.
• Reentry-phase trajectory runs produced representative outputs, but they were not fully converged/validated and should be treated as illustrative.
• Defined a Monte Carlo + KDE workflow for impact probability mapping as the next integration step.

2) Motivation

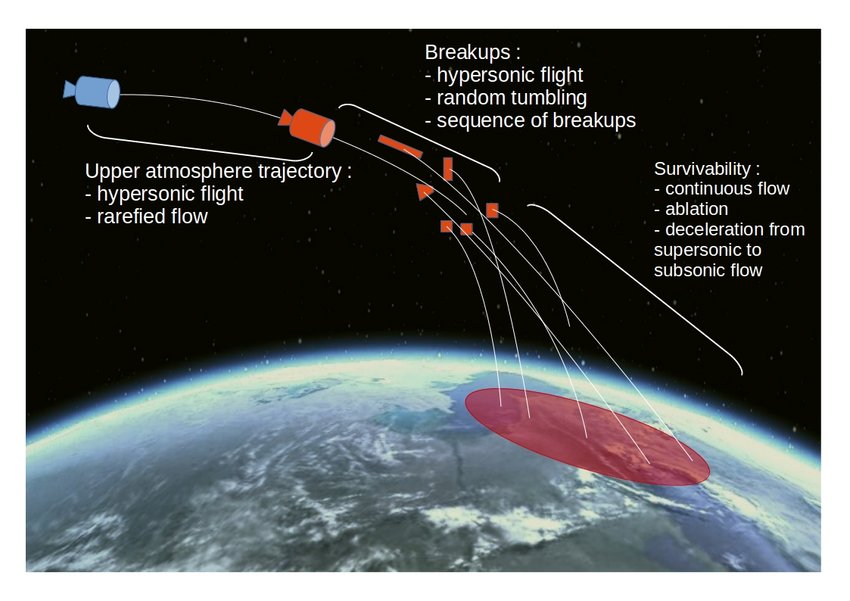
Predicting uncontrolled reentry matters for public safety, mission operations, and post-mission risk communication. Even when nominal decay timing is understood, atmospheric variability, aerodynamic uncertainty, and breakup physics can widen uncertainty in final ground impact location.

This project focused on the modeling backbone needed to reduce that uncertainty over time and make assumptions explicit. Below is an example of a debris piece from space that crashed through a house in Florida in 2021. It was over 4 inches tall!

Illustrative motivation visual: reentry prediction is fundamentally a risk and uncertainty management problem.

3) Project Overview

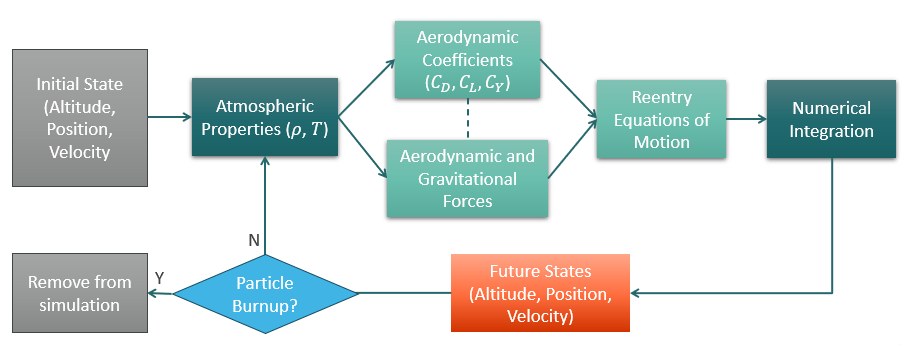
IMPART is an integrated architecture with three linked phases:

1. Orbit Decay (>~100 km): propagate ECI state with gravity + drag using atmospheric density models and ode113.
2. Reentry (~100 km down): propagate a low-fidelity 3DOF reentry model with J2 gravity + aerodynamic loads using fixed-step RK4.
3. Impact Footprint (concept): sample uncertainty via Monte Carlo and convert terminal points into a 2D probability map using KDE.

Scope assumptions:

• Point-mass translational dynamics (no full attitude coupling).
• Constant aerodynamic coefficients in the current reentry phase (CD, CL, CY).
• No breakup/heating coupling in the present solver chain.

Reentry context visuals used to frame phase boundaries and survivability assumptions.

Orbital decay geometry and trajectory visualization used to communicate phase-1 behavior.

4) Methods

4.1 Atmospheric Density Modeling (Analytical vs NRLMSISE-00)

I implemented two atmosphere options:

1. An analytical baseline model for quick parametric checks.
2. NRLMSISE-00 through MATLAB atmosnrlmsise00 for altitude/time-varying density and temperature behavior.

The dual-model approach made it possible to benchmark sensitivity and quickly identify where simplified assumptions break down.

4.2 Orbit Decay Dynamics (>100 km)

The decay model propagated the inertial state in ECI with:

• Two-body gravity.
• Aerodynamic drag using local density and relative atmospheric velocity.

Relative airspeed was computed as V_A = |V - (omega_E x r)|, and drag acceleration followed the standard ballistic form using rho, CD, reference area, and mass. Time integration used ode113 for stable long-horizon propagation through the high-altitude regime.

4.3 Reentry Dynamics (~100 km down)

The reentry phase used a low-fidelity 3DOF translational model including:

• Gravity with J2 correction.
• Aerodynamic force components based on constant CD, CL, and CY.
• Fixed-step RK4 integration for explicit control of step size and phase transition handling.

This phase was intended as a first-principles prototype rather than a high-fidelity flight-certified model.

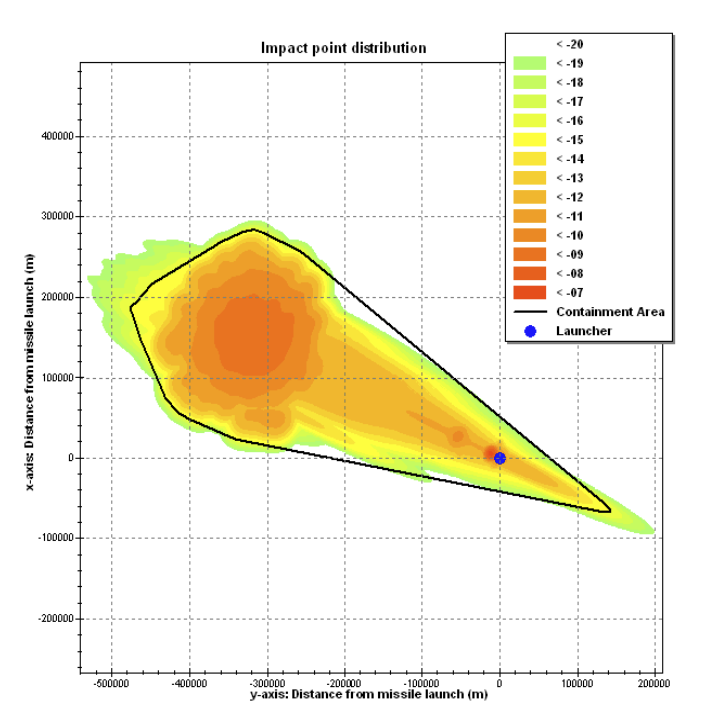
4.4 Impact Footprint Concept (Monte Carlo + KDE workflow)

The planned footprint workflow was:

1. Sample uncertain initial conditions and model parameters.
2. Propagate each sample through the terminal dynamics chain.
3. Collect terminal ground points.
4. Apply KDE to generate a 2D impact-probability surface and containment contours.

The architecture and target outputs were defined, with full end-to-end execution positioned as follow-on work.

5) Implementation Notes

The framework was implemented as modular MATLAB/Simulink components so atmosphere, force models, and numerical solvers could be swapped independently without rewriting the full pipeline.

Key implementation choices:

• ode113 for orbital decay phase (variable-step, smooth long-span propagation).
• Custom fixed-step RK4 for reentry phase (explicit control and reproducibility).
• Shared state/parameter handoff between phases at the ~100 km transition altitude.
• Constant aerodynamic coefficients and no coupled thermal/breakup dynamics in the current reentry block.

Left: IMPART model flow (state -> atmosphere -> aero/gravity -> EOM -> integration). Right: literature-style reference architecture that informed decomposition.

6) Results

6.1 Density model comparisons

NRLMSISE-00 captured altitude and time-of-day structure that is not represented by simple analytical baselines, especially across broader altitude spans.

Density and temperature comparisons from analytical and NRLMSISE-00 runs across altitude regimes.

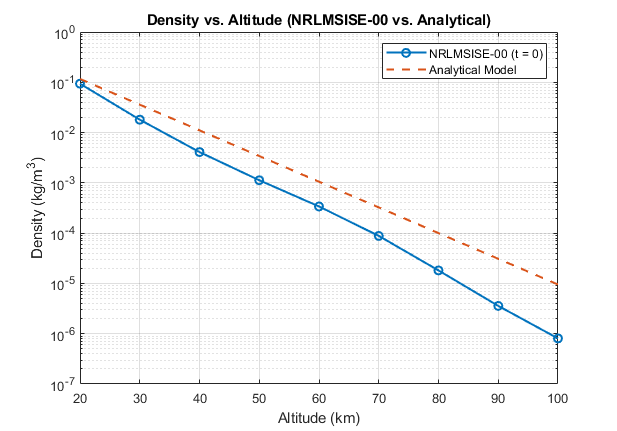
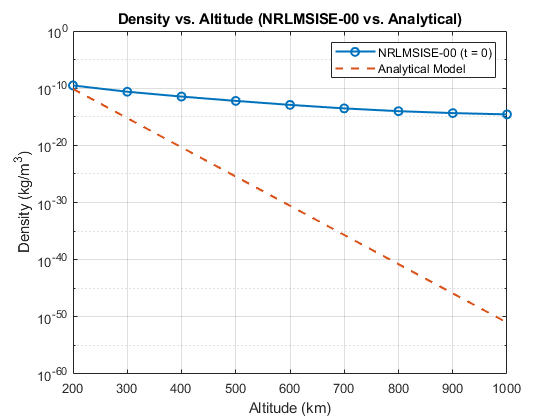
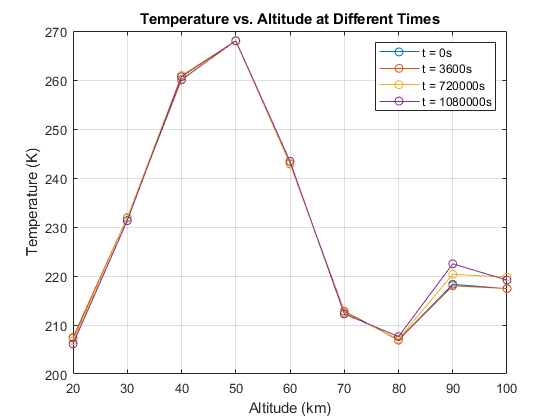
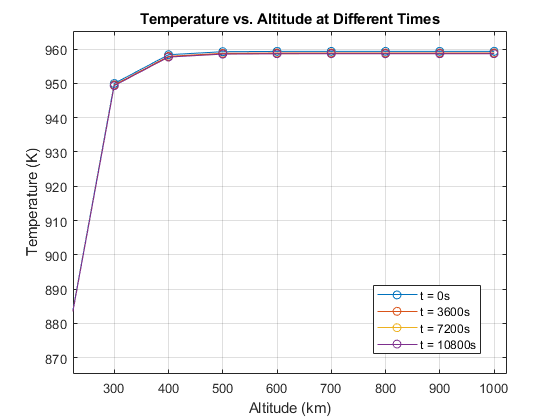
6.2 Orbit decay cases + sensitivity (baseline / low mass / lower start altitude)

The decay solver produced expected trend behavior:

• Baseline case showed smooth altitude loss over time.
• Lower mass case increased drag sensitivity and accelerated decay.
• Lower initial altitude case reduced remaining orbital lifetime.

Altitude-time decay results for baseline and two sensitivity cases.

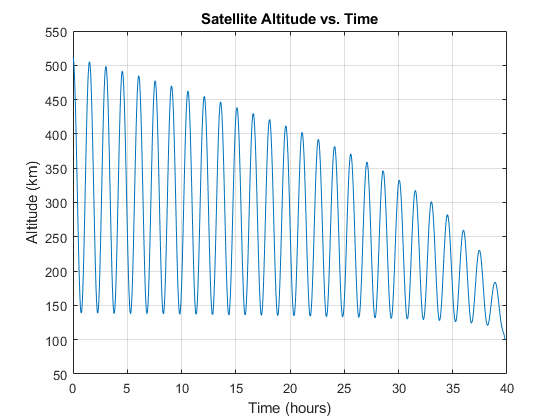
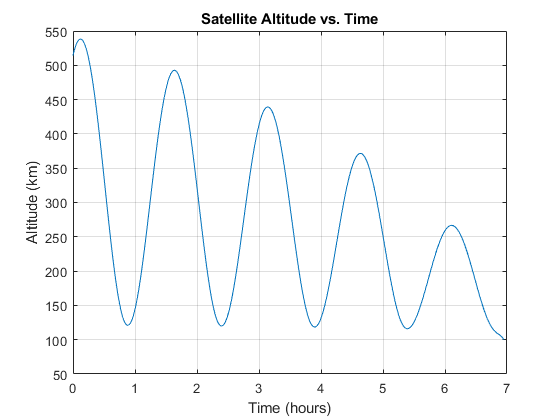
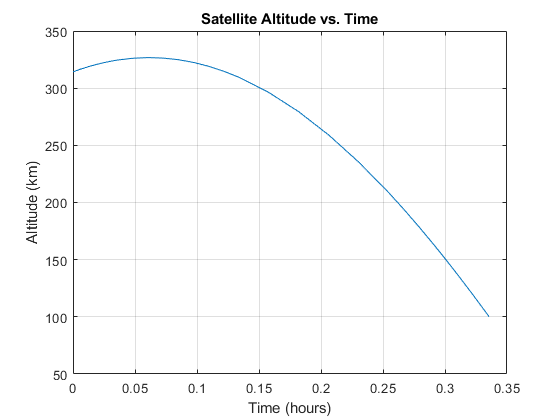
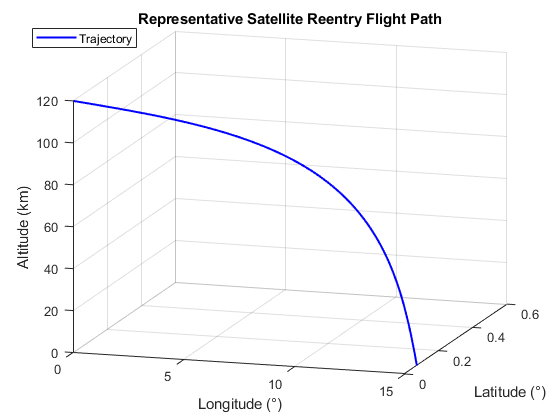
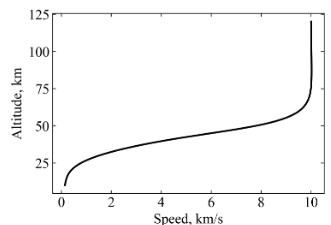
6.3 Reentry trajectory outputs

The reentry plots below are representative outputs from the current 3DOF solver chain.

Important caveat: these reentry-stage trajectories were not fully validated and showed non-converging behavior in some runs. They are useful for debugging/model-development context, not final predictive claims.

Likely contributors include integrator setup sensitivity, phase-transition conditioning, and low-fidelity aerodynamic assumptions.

Representative reentry outputs from current implementation (illustrative only; not fully validated).

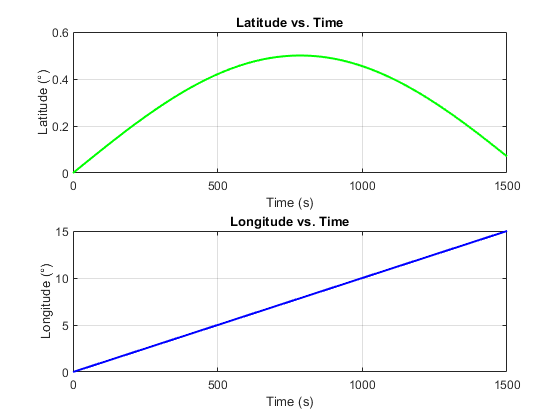
7) Limitations & What I’d Fix Next

• Tighten phase-transition logic around ~100 km to avoid state discontinuity and step-size artifacts.
• Run RK4 step-size convergence sweeps and compare against an independent adaptive integrator.
• Replace constant aero coefficients with altitude/Mach/attitude-dependent aerodynamic data.
• Add unit/integration tests for force-model consistency and conserved-quantity checks where applicable.
• Add verification cases with known analytical/benchmark trajectories before claiming predictive fidelity.

8) Future Work

Planned next steps:

• Complete end-to-end Monte Carlo + KDE footprint generation with containment metrics.
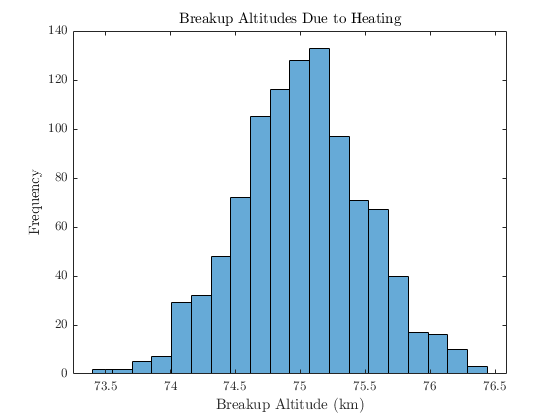
• Add breakup and heating logic to couple terminal dynamics with fragment survivability.
• Expand aerodynamic modeling (coefficient tables, regime switching, uncertainty bounds).
• Build a validation plan against historical reentry events and published benchmark scenarios.

Left: breakup uncertainty context. Right: example of target ground-impact probability output.

Feel free to reach out to discuss this project more!